[IA]
anno 20 numero 39 / 10.25
Biografie
Elena Agliari, laureata e dottorata in fisica all’Università di Parma, è professoressa in fisica matematica presso il Dipartimento di Matematica dell’Università Sapienza di Roma, dove insegna modelli di reti neurali e matematica per il machine learning. Si è occupata di processi di diffusione su grafi, modelli matematici applicati alle reti immunitarie e di meccanica statistica dei sistemi disordinati.
Adriano Barra, laureato in fisica presso la Sapienza Università di Roma e dottorato in matematica presso la King’s College University of London, è professore associato in fisica matematica presso il Dipartimento di Scienze di Base e Applicate per l’Ingegneria (SBAI) della Sapienza, dove tiene un corso di reti neurali e machine learning per il dottorato. La sua ricerca verte prevalentemente su meccanica statistica di reti neurali e sistemi disordinati e modellizzazione matematica di fenomeni biologici.
Cogito ergo \sum
Il ruolo della meccanica statistica nelle reti neurali
di Elena Agliari e Adriano Barra

a.
Il premio Nobel Giorgio Parisi, padre della meccanica statistica dei sistemi complessi (tra i cui esempi più celebri si annoverano le reti neurali).
Gli anni ’70 dello scorso secolo sono stati storiograficamente catalogati come l’inverno (“winter time”) dell’IA. Proviamo a comprenderne le ragioni e ad analizzare come questa apparente stagnazione abbia in realtà favorito una profonda maturazione del campo, enfatizzando il ruolo che la fisica ha svolto nel condurre la ricerca verso una nuova primavera.
Nel 1970 erano ormai lontane le prime decadi del secolo in cui Ivan Pavlov costruiva le leggi teoriche della fisiologia, studiando il riflesso condizionato nei cani, mentre Santiago Ramon y Cajal e Camillo Golgi sviluppavano tecniche sperimentali per mettere in luce la morfologia del singolo neurone. Si erano anche già succeduti i primi modelli matematici di neurone, celebre quello di McCulloch e Pitts del ’43, ed era già comparso il percettrone di Rosenblatt nel ’58, una macchina che ne imita le caratteristiche computazionali. Semplificando, possiamo schematizzare un neurone come un interruttore, che alterna uno stato quiescente – quando la corrente ad esso afferente dai neuroni adiacenti non raggiunge una prestabilita soglia – e uno attivo, in cui tale soglia viene raggiunta e gli permette l’emissione di un impulso elettrico veicolato verso i neuroni ad esso connessi (vd. approfondimento).
La natura elettrica della comunicazione neuronale e i primi modelli matematici si innestavano perfettamente nella logica di Boole (formalizzata a metà dell’800), portando a concepire, nella prima metà del secolo scorso, l’elaborazione dell’informazione nelle reti neurali come l’esecuzione di protocolli deterministici di operazioni logiche. Questa idea andò in frantumi nel ’69, quando Marvin Minsky e Seymour Papert mostrarono che il percettrone di Rosenblatt non era in grado di riprodurre tutte le funzioni logiche di base, congelando gli entusiasmi della comunità scientifica.
Il conseguente winter time segnò, in realtà, una profonda rivoluzione culturale che consentì, tacitamente, la transizione dal primo al secondo programma per l’IA. Infatti, si realizzò presto che, mentre un singolo percettrone non è in grado di simulare tutte le funzioni logiche fondamentali, un insieme di pochi percettroni opportunamente connessi sa farlo, e questo spostava l’attenzione dal soggetto (il neurone) alla rete delle sue interazioni (la rete neurale, vd. approfondimento), dando avvio a un significativo ammodernamento del bagaglio metodologico-scientifico sottostante alla loro trattazione. La logica matematica e la neonata cibernetica venivano affiancate da discipline in grado di cogliere le proprietà emergenti in grandi “collezioni” di elementi semplici, come la meccanica statistica, l’inferenza statistica (un insieme di metodi che permettono di trarre conclusioni su una popolazione più ampia basandosi sui dati raccolti da un campione) e la teoria dei grafi.
Per enfatizzare la portata del cambiamento di paradigma, per dirla con il filosofo Thomas Kuhn, notiamo che la (storicamente celebre) rivoluzione copernicana del passaggio dal sistema geocentrico al sistema eliocentrico, spostava l’attenzione da un soggetto (la Terra) a un altro (il Sole), mentre nel cambio che stiamo discutendo il focus si sposta dai soggetti alle loro interazioni: un significativo salto concettuale tanto che, ad oggi, quasi la totalità della Natura è stata ripensata in termini di reti di interazioni.

b.
Daniel Amit, pioniere delle reti neurali. Haim Sompolinsky e Hanoch Gutfreund e lo stesso Amit negli anni ’80 furono i primi a usare la meccanica statistica delle reti frustrate per descrivere esaustivamente le proprietà di processazione d’informazione delle reti neurali, e in particolare nel modello di Hopfield. Amit è stato professore del corso sulle reti neurali alla Sapienza Università di Roma fino al 2007.
È importante ricordare che la meccanica statistica, nata sul chiudersi della Belle Époque e già ben consolidata negli anni ’70, sapeva trattare esaurientemente reti di elementi binari (i.e. “spin a due stati”) in interazione semplice (ad esempio, spin che tendono ad allinearsi se l’agitazione termica lo consente), mentre per reti “frustrate” (in cui coesistono interazioni “cooperative” che favoriscono l’allineamento tra due spin e interazioni “anti-cooperative”, che ne favoriscono l’anti-allineamento) non esistevano ancora gli strumenti teorici e matematici necessari per affrontarne lo studio.
Il giusto riferimento modellistico nella meccanica statistica era però proprio quello delle reti frustrate poiché, interpretando i nodi della rete (i.e. gli spin) come neuroni a due stati (on/off) e le connessioni tra essi come sinapsi, era imprescindibile considerare modelli con interazioni sia cooperative che anti-cooperative, dato che nelle reti neurali esistono sia sinapsi eccitatorie che inibitorie. Da questo punto di vista, gli anni ’70 furono una vera fucina di idee e di concetti preliminari all’edificazione di una meccanica statistica capace di descrivere quantitativamente il comportamento di tali sistemi complessi. Un decisivo punto di sintesi si raggiunse a cavallo tra gli anni ’70 e ’80, quando Giorgio Parisi sviluppò la sua celebre teoria che gli valse il premio Nobel per la fisica nel 2021, nella quale la compresenza di stimoli cooperativi e anti-cooperativi genera un “paesaggio” altamente non banale di minimi dell’energia. La meccanica statistica aveva così subito una trasformazione radicale, che si manifestava su più fronti. In primis, l’introduzione delle reti frustrate ne ampliò lo spettro applicativo ben oltre la fisica, suo ambito originario. In secondo luogo, venne codificato un nuovo vocabolario di osservabili e concetti (ad esempio “overlap” (sovrapposizione), “replica”, “simmetria di replica” e sua “rottura”) oggi di uso comune in informatica teorica e indispensabili per l’inferenza statistica in spazi ad alta dimensionalità, entrambi pilastri metodologici della moderna intelligenza artificiale.
Non si dovette quindi aspettare molto per veder nascere i primi modelli di rete neurale, da quello proposto da Hopfield nel 1982 (che implementava le idee sull’apprendimento di Donald Hebb, a loro volta sintesi degli studi di Pavlov), alla “macchina di Boltzmann”, il prototipo formulato da David Ackley, Geoffrey Hinton e Terrence Sejnowski nel 1985 (che sintetizza il ruolo egemone della meccanica statistica già nel suo nome, facendo riferimento a Ludwig Boltzmann). A cascata, tra il 1985 ed il 1987, Daniel Amit, Hanoch Gutfreund e Haim Sompolinsky pubblicavano la prima trattazione sistematica, interamente meccanico-statistica, di queste reti neurali, proprio sfruttando i concetti e le tecniche dei sistemi frustrati di Parisi: capito come associare ai minimi dell’energia le informazioni da immagazzinare, i.e. i pattern (vd. fig. 1a), queste reti potevano funzionare come memorie associative nelle quali richiamare un pattern (p.es. un’immagine) precedentemente appreso. Questo significava raggiungere spontaneamente uno degli stati di minimo (o di equilibrio) a seguito di un opportuno stimolo: tale cruciale capacità è diventata celebre con il nome di “pattern recognition” (vd. fig. 1b).
La meccanica statistica si consolidava così come disciplina cardine del settore, consacrata, oltre al Nobel a Parisi nel 2021, dal Nobel per la fisica conferito lo scorso anno a Hopfield e Hinton per i loro studi pioneristici su questi sistemi. Inoltre, vale la pena ricordare che, nel versante puramente matematico, l’importanza di questi studi è stata suggellata con l’assegnazione, sempre nel 2024, del premio Abel a Michel Talagrand, anche per aver dimostrato rigorosamente la correttezza della formulazione parisiana dei sistemi complessi.

c.
Francesco Guerra, recentemente scomparso, è stato lo scienziato che, lavorando all’intersezione tra la fisica teorica e la matematica, ha sistematicamente gettato le basi metodologiche per rendere la teoria di Parisi matematicamente impeccabile, contribuendo in maniera cruciale alla sua riformulazione in termini di teoremi matematici.
Una curiosità storica riguarda la fisica teorica napoletana: precursore del modello di Hopfield è il modello di Shun’ichi Amari, un fisico giapponese sovente invitato da Eduardo Caianiello, fisico teorico napoletano, a spendere mesi in Costiera Amalfitana negli anni ’60. Caianiello ed Amari si influenzarono reciprocamente e anticiparono i primi concetti sulle future teorie delle reti neurali. Tre decadi dopo, fu Francesco Guerra, di cui Caianiello fu mentore accademico, a costruire una serie di tecniche matematiche che permisero di dimostrare rigorosamente la teoria di Parisi, aprendo de facto la strada al premio Abel a Talagrand.
L’ampio intervallo di tempo che intercorre tra la formulazione di questi modelli e il conferimento del Nobel ai loro autori non deve sorprendere: questo è dipeso dal fatto che, quando la teoria venne edificata, non era sostanzialmente possibile metterla alla prova. Fino a un paio di decadi fa, non esisteva un mondo digitale in cui le reti neurali artificiali potessero apprendere.
[as] approfondimento
Il modello di Hopfield
1.
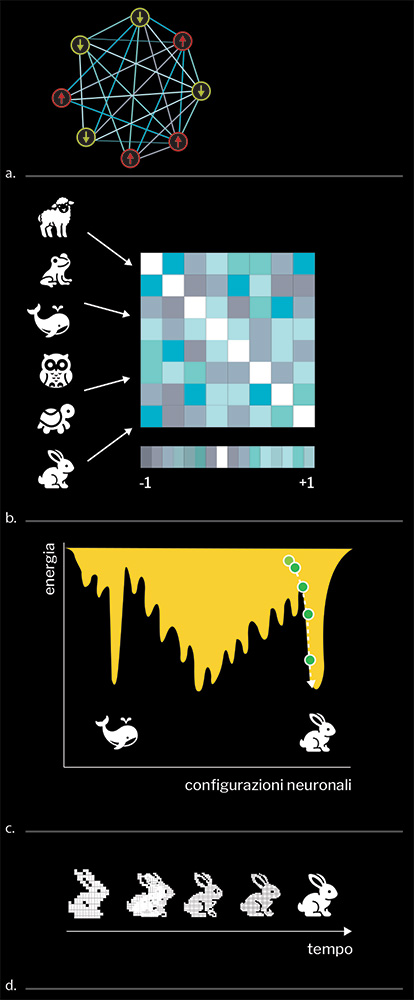
a) Grafo rappresentante una rete neurale composta da otto neuroni. b) Pattern da memorizzare e relativa matrice sinaptica con scala delle intensità. c) Panorama energetico della rete neurale. d) Evoluzione temporale della configurazione neurale, che realizza la ricostruzione di uno dei pattern immagazzinati nella matrice sinaptica.
Un sistema di unità interagenti può essere visualizzato attraverso un grafo, ovvero una rete in cui i nodi rappresentano le unità (per esempio neuroni) e le connessioni indicano l’esistenza di un’interazione (per esempio la presenza di una giunzione sinaptica). In fig. 1a è mostrata una rete neurale, in cui i neuroni evidenziano la loro modellizzazione mediante variabili binarie (i.e. “spin up/spin down”). Nel modello di Hopfield le intensità delle interazioni tra i neuroni sono determinate in maniera tale che la rete manifesti proprietà collettive che riproducono il funzionamento di una memoria associativa, ovvero la capacità di ricostruire un’informazione quando questa viene mostrata in maniera parziale o rumorosa. Le informazioni da memorizzare, per esempio una serie di immagini in bianco e nero, anche dette pattern, vengono opportunamente sommate (da cui è nato il titolo di questo articolo, dove “sum” non è un errore ma indica l’operazione della “somma” in LaTeX, il linguaggio con cui gli scienziati scrivono i loro articoli), in modo da ottenere la “matrice sinaptica”, ovvero una matrice i cui ingressi corrispondono alle intensità dell’interazione tra i nodi corrispondenti. Per esempio, in fig. 1b l’interazione tra il neurone 3 ed il neurone 5, corrispondente all’ingresso (3,5), è negativa e relativamente intensa (con un valore vicino a -1, secondo la scala di colore indicata nella parte bassa). Data una rete e specificate le interazioni tra i suoi elementi, è possibile associare ad ogni configurazione neuronale, che specifica quali neuroni sono attivi e quali neuroni sono a riposo, un’energia ovvero un “costo”, ottenendo un “paesaggio energetico” come quello mostrato in fig. 1c. Il fatto che la matrice sinaptica abbia sia ingressi positivi che negativi definisce tale rete come frustrata e, di conseguenza, il paesaggio dell’energia ad essa associata appare corrugato, denso di minimi. Per far funzionare la rete è ora necessario introdurre una regola evolutiva per lo stato dei neuroni che assicuri la convergenza spontanea della rete da uno stato di input (p.es. l’immagine corrotta del coniglio) allo stato di output desiderato (l’immagine pulita del coniglio). Sotto opportune condizioni, la matrice sinaptica descritta prima realizza un panorama energetico tale che i minimi corrispondono a configurazioni neurali che riproducono i vari pattern incamerati. La regola evolutiva sarà allora particolarmente semplice: muoviti nella direzione che riduce il valore della funzione costo, cioè aggiorna lo stato di un neurone solo se ciò comporta una riduzione energetica. Un esempio di traiettoria è riportato in fig. 1c, insieme alla corrispondente ricostruzione del pattern “coniglio” in fig. 1d.
Biografie Elena Agliari, laureata e dottorata in fisica all’Università di Parma, è professoressa in fisica matematica presso il Dipartimento di Matematica dell’Università Sapienza di Roma, dove insegna modelli di reti neurali e matematica per il machine learning. Si è occupata di processi di diffusione su grafi, modelli matematici applicati alle reti immunitarie e di meccanica statistica dei sistemi disordinati. Adriano Barra, laureato in fisica presso la Sapienza Università di Roma e dottorato in matematica presso la King’s College University of London, è professore associato in fisica matematica presso il Dipartimento di Scienze di Base e Applicate per l’Ingegneria (SBAI) della Sapienza, dove tiene un corso di reti neurali e machine learning per il dottorato. La sua ricerca verte prevalentemente su meccanica statistica di reti neurali e sistemi disordinati e modellizzazione matematica di fenomeni biologici.


