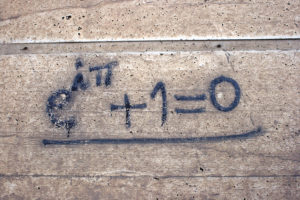Segni sognanti

Nella raccolta “Poesia in forma di rosa” Pier Paolo Pasolini parla di “escogitare un sistema di segni, sistemare un sistema di segni, trovare segni una volta per sempre internazionali e scoperchiare segni sognanti”. La stessa evoluzione si può applicare ai segni di cui la matematica è piena, schierandosi tra coloro che pensano che gli oggetti del suo linguaggio si inventino e non si scoprano.

Ogni segno matematico ha una sua storia che parte dal momento di necessaria introduzione o di casuale intuizione, passa per la sua affermazione nella comunità scientifica e l’uso dello stesso simbolo in universi matematici differenti, e arriva al racconto divulgativo.
Racconti interessantissimi, come quello dell’“identità di Eulero”, l’equazione definita dal fisico Richard Feynman la “formula più bella della matematica”: e^iπ + 1 = 0. In tanti oggi scelgono questa formula come tatuaggio, forse perché sembra un viaggio disordinato nello spazio e nel tempo: c’è l’unità dei greci antichi e i cerchi di Archimede; lo “zefiro” arabo, zero degli indiani in Oriente e “spazio vuoto” nelle tavole Babilonesi e dei Maya; gli studi inglesi seicenteschi sui logaritmi e le funzioni esponenziali degli svizzeri settecenteschi, c’è l’Ars Magna dell’italiano Cardano e la Germania di Gauss.
La storia del lungo viaggio dello zero sulle navi pisane per poi abitare le borse mondiali e i computer di ogni casa ci fa render conto di come “escogitare un sistema di segni” con lo zero sia stata una idea straordinaria.
Il numero “uno”, invece, ha una origine concettuale talmente innata che raccontarne genesi e utilizzi sarebbe impensabile. Ogni ambito del sapere (dalla biochimica alla sociologia) ha “sistemato il suo sistema di segni” includendo l’unità.
Pi-greco (π) è al contrario un segno molto tardivo rispetto al problema che lo definisce da millenni: il rapporto invariante tra la circonferenza e il suo diametro, che ha ispirato tanti matematici per la sua approssimazione, fu denotato con solo π nel 1706 in uno scritto di William Jones. Questo segno divenne “per sempre internazionale”, grazie all’utilizzo continuo che ne fece nello stesso secolo il grande matematico Leonhard Euler (in italiano noto come Eulero).
Il nostro sistema matematico di segni diventa “sognante”, se conduce oltre l’esperienza del reale, e questo accade ogni volta che si ha a che fare con l’infinito. La traccia grafica dell’infinito è nei numeri irrazionali, che corrispondono a rapporti geometrici, come ad esempio quello tra lato e diagonale in un quadrato. Per quanto i pitagorici volessero negare l’evidenza della cosa, ogni volta che disegniamo un quadrato o la stella di diagonali in un pentagono regolare, l’infinito ci guarda dal foglio e ci interroga.
La domanda diventa sfidante se tracciamo la circonferenza e il suo diametro: “c’è infinito in questo rapporto?”, chiedeva il foglio fino alla fine del ’700. E il matematico faceva scena muta. Tenendo conto che il genere Homo ha tracciato cerchi già 40.000 anni fa, si tratta della più lunga interrogazione della storia!

A saper rispondere fu Eulero, il quale, applicando alla geometria somme e prodotti infiniti, risolse nel 1735 il problema di Basilea e ottenne π (al quadrato diviso 6) mediante una meravigliosa somma dei reciproci degli interi al quadrato. Il suo collega Johann H. Lambert usò simili argomenti per dimostrarne l’irrazionalità.

Dopo un processo limite di Jean Bernoulli, in un calcolo di Christiaan Huygens l’area unitaria sotto l’iperbole rettangolare poneva analoghe domande: la costante che Eulero, in una lettera a Goldbach del 1731, aveva indicato con “e”, la base per i logaritmi prediletta da Giovanni Nepero, si poteva rappresentare elegantemente come somma di infiniti termini? Da questi segni sognanti si poteva dedurne l’irrazionalità? Anche in questo caso Eulero trovò l’elegante serie di reciproci dei fattoriali per dimostrare entrambe le cose. Ma la passione di Eulero per le serie non finì qui, ottenne lo sviluppo delle funzioni seno e coseno e si accorse che la loro combinazione conduceva proprio a quella del numero di Nepero e, a condizione di sistemare i segni alterni. A tale scopo usò l’unità immaginaria “i”, la cui caratteristica è che i² = -1. Questa era stata introdotta solo formalmente per far tornare la molteplicità delle soluzioni delle equazioni polinomiali. Anzi, fu proprio lui ad assegnare una vocale, come già fatto per e, al più sognante e discusso dei segni matematici. Questo gli consentì di riscrivere quelle somme infinite nella breve formula e^iθ = cos θ + i sin θ.
Ma quale geometria raccontavano questi segni escogitati? Si sistemavano in un’immagine? Dalla formula bisognava tornare a guardare il foglio e passare alla forma.
Così come Pasolini aveva detto “scoperchiare segni sognanti”, così Carl Friedrich Gauss aveva scoperchiato il piano cartesiano, mostrando l’universo dei numeri complessi. In questo nuovo mondo, θ diventa un angolo, mentre e^iθ si situa sulla circonferenza unitaria. Basta quindi mettere θ = π, ricordare che cos π = -1 e sin π = 0 ed ecco che in poche battute ritroviamo la protagonista della nostra storia: e^iπ + 1 = 0.
Filosoficamente, stiamo parlando di una formula un po’ platonica e un po’ realista, che racchiude sia l’uguaglianza e la somma, nate con l’uomo stesso, che la moltiplicazione e l’elevamento a potenza, introdotte per semplificare i calcoli, oltre alla geometria del piano e la fisica delle onde. Come diceva Pasolini, “per essere poeti bisogna avere molto tempo”, ma di certo non ne serve di meno per essere scienziati!