La rivincita del disordine

La costante di Boltzmann

di Irene Giardina

a.
“Passeggiata costante di Boltzmann”, opera su legno fimo e olio di Roberto Zingoni. La scultura raffigura la traiettoria del moto browniano di una particella, a partire dalla quale è stato misurato il valore della costante di Boltzmann.

La termodinamica nacque all’inizio dell’800 come la teoria che descrive le trasformazioni che coinvolgono calore e lavoro. Il calore rappresenta una forma di energia, la cui conservazione viene stabilita dal primo principio della termodinamica. Nella seconda metà dell’800 l’interesse si spostò invece verso lo studio di quali processi termodinamici possono avvenire e quali no e su quali fenomeni e trasformazioni possano avvenire spontaneamente e quali no, portando così alla formulazione del secondo principio della termodinamica. L’introduzione del concetto di “entropia” e il collegamento con la teoria microscopica dei gas hanno origine proprio in quegli anni dai contributi fondamentali di Rudolf Clausius, Planck e in particolare di Ludwig Boltzmann (vd.[as] radici: Tra meccanica e termodinamica, ndr.). Ed è qui che entra in gioco la costante di Boltzmann k_B, che collega la termodinamica a un’altra fondamentale branca della fisica, la meccanica statistica, che studia il comportamento di sistemi composti da tantissime molecole. Questo collegamento avviene attraverso delle leggi estremamente eleganti che hanno implicazioni più ampie, arrivando a coinvolgere anche concetti come il disordine e l’informazione.
In termodinamica, k_B ha innanzitutto il compito cruciale di legare tra loro la temperatura assoluta (T) di un sistema e la sua energia interna, permettendoci di collegare l’una con l’altra. Questa connessione compare già nella celebre legge dei gas perfetti PV = N k_B T (dove P è la pressione, V il volume e N il numero di molecole), formulata nella prima metà dell’800 a partire dalle osservazioni sperimentali di Robert Boyle, Joseph L. Gay-Lussac, Émile Clapeyron e altri fisici dell’epoca.

c.
Nella prima metà del ’900 Claude Shannon (in foto) ha sviluppato un concetto alternativo di entropia nel contesto della teoria dell’informazione.

Questa equazione mostra che il prodotto di k_B con T ha le dimensioni fisiche di un’energia e fornisce la scala energetica tipica di una particella in un gas a pressione e volume dati. Ciò è ancora più evidente nell’espressione esplicita dell’energia interna di un gas perfetto, ottenuta con la teoria cinetica da Maxwell e Ludwig Boltzmann nella seconda metà dell’800, in cui l’energia del gas risulta proporzionale proprio al numero di molecole e al prodotto di k_B con T.

Il ruolo più significativo della costante di Boltzmann, nonché quello con maggiore rilevanza nelle applicazioni moderne, è legato però a un’altra quantità fisica, l’“entropia”. Esistono varie definizioni di entropia e ognuna è per certi aspetti rilevante per la sua comprensione. In termodinamica, il concetto di entropia è dovuto a Clausius, che la introdusse come funzione di stato (una grandezza che permette di definire lo stato di un sistema) e ne diede una definizione operativa legando le variazioni di entropia al rapporto tra il calore scambiato dal sistema e la sua temperatura. Usando l’entropia, il secondo principio della termodinamica asserisce che in un sistema isolato l’entropia non può mai diminuire. Questa relazione stabilisce una direzione del tempo (quella in cui l’entropia aumenta) e sancisce la natura irreversibile della termodinamica. Per capire dove entri in gioco la costante di Boltzmann e per comprendere meglio il significato dell’entropia, possiamo usare un esempio classico: l’espansione libera di un gas perfetto (vd. fig. b). Consideriamo un contenitore isolato, diviso in due volumi uguali da un setto rimovibile e mettiamo tutto il gas in una delle due parti. Se rimuoviamo il setto, il gas si espanderà fino a occupare l’intero volume. Un semplice calcolo mostra che, come prescritto dal secondo principio della termodinamica, l’entropia del gas aumenta. La sua variazione è proporzionale alla costante di Boltzmann e ha le sue stesse dimensioni fisiche (ossia di un’energia divisa per una temperatura).

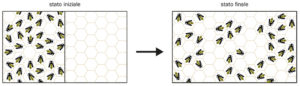
b.
Esempio di aumento di entropia. Inizialmente le api sono vincolate a stare tutte in un settore dell’alveare (configurazione a bassa entropia). Se togliamo il vincolo, possono muoversi liberamente in tutto lo spazio disponibile e con alta probabilità lo occuperanno in modo uniforme, aumentando l’entropia. Il corrispettivo termodinamico di questo esempio è l’espansione libera di un gas.

Essa, inoltre, dipende dal rapporto tra il volume finale occupato dal gas e quello iniziale, suggerendo che l’entropia misuri in qualche modo lo spazio accessibile alle particelle che lo compongono. Questo aspetto è caratterizzato in modo più preciso e generale nelle definizioni di entropia formulate nel contesto della meccanica statistica.

La meccanica statistica si pone come obiettivo di ricavare le leggi termodinamiche a partire dalle proprietà microscopiche del sistema attraverso una teoria di tipo probabilistico. Quando un sistema macroscopico (composto, ad esempio, da tante molecole) si trova in uno stato di equilibrio, esso in realtà esplora molti stati microscopici (delle singole molecole), tutti coerenti con le variabili termodinamiche misurate. Per esempio, un gas in equilibrio, contenuto in un recipiente isolato, è in uno stato macroscopico definito dal volume che occupa e dalla temperatura, che è una misura del suo contenuto energetico. A parità di volume e temperatura, le molecole che continuano incessantemente a muoversi possono trovarsi in tante configurazioni diverse, che noi non riusciamo a distinguere singolarmente. La meccanica statistica assegna una probabilità a ciascuno di questi microstati. Se vi sono in tutto W microstati con energia e volume dati, l’ipotesi più semplice è che il gas esplori con la stessa probabilità ognuno di essi. In questo caso, l’entropia di Boltzmann è definita da una famosa equazione: S = k_B log W. È proprio in questa definizione, dovuta ai lavori di Boltzmann e formulata da Planck, che la costante di Boltzmann compare per la prima volta. Da questa espressione capiamo quanto intuìto nell’esempio dell’espansione libera, menzionato in precedenza: l’entropia quantifica il numero di microstati accessibili al nostro sistema (la quantità W) e k_B è la costante che traduce questa misura in una grandezza di valenza termodinamica, l’entropia S.
Josiah Willard Gibbs successivamente propose un’ulteriore definizione di entropia che generalizza quella di Boltzmann a sistemi con condizioni macroscopiche diverse, in cui le probabilità dei singoli microstati non sono più tutte uguali. Per esempio, consideriamo un gas che non sia isolato, ma in contatto termico con un ambiente esterno. All’equilibrio, il gas avrà un’energia interna ben definita, che possiamo misurare. Tuttavia, nei singoli microstati che esso esplora continuamente l’energia può avere delle piccole fluttuazioni dovute all’interazione con l’esterno, e ognuno di essi avrà una probabilità diversa.
Anche in questo caso, tale probabilità rappresenta l’indeterminazione statistica di uno stato microscopico del sistema. Seguendo la stessa filosofia di Boltzmann, l’entropia introdotta da Gibbs misura il valore medio di questa incertezza. Da questo punto di vista possiamo dunque dire che l’entropia misura la quantità di informazione, necessaria per specificare completamente lo stato microscopico del sistema.
La connessione tra entropia termodinamica e informazione assume un ruolo ancora più importante, se consideriamo un altro concetto di entropia sviluppato nella prima metà del ’900 da Claude Shannon proprio nel contesto della teoria dell’informazione. Preso un set di dati, Shannon si chiese quale fosse il modo più conveniente di comprimerli. Egli calcolò dunque il numero minimo di bit informatici necessario per codificare il set di dati, ossia il suo contenuto di informazione. Questa quantità è la cosiddetta “entropia di Shannon”. Se adesso, facendo un parallelismo con quanto discusso precedentemente, consideriamo come set di dati l’insieme dei microstati di un sistema termodinamico, possiamo calcolare su di essi sia l’entropia termodinamica di Gibbs, sia l’entropia di Shannon e vedere quale sia la relazione tra le due. Come intuìto in precedenza, l’entropia di Gibbs risulta essere proporzionale all’informazione contenuta nel sistema, e k_B è la costante che dà a tale quantità di informazione dimensioni termodinamiche. Si trova infatti che alla perdita di 1 bit di informazione corrisponde una variazione di entropia pari a k_B log 2. Partendo da questa osservazione, Rolf Landauer argomentò nel 1961 che, in generale, l’energia minima necessaria per distruggere 1 bit di informazione per un computer che opera alla temperatura T è quantificabile: è proprio pari a k_BT log 2. Questo principio, noto come “principio di Landauer”, ha importanti implicazioni nel campo della computazione. I computer operano infatti registrando e distruggendo informazione. Molte operazioni logiche fondamentali, che vengono chiamate “logicamente irreversibili”, corrispondono alla cancellazione di informazione. Il principio di Landauer pone dunque un limite teorico minimo all’energia consumata da un computer per il suo funzionamento.
La costante di Boltzmann si rivela quindi una chiave fondamentale per comprendere il legame profondo tra entropia, informazione e computazione, con implicazioni che vanno ben oltre lo studio della termodinamica dei sistemi macroscopici.